GPU 的内部并不存在一个真实的物理世界，像真实摄影一样得出模型的光照和颜色。所有像素的亮度、颜色都需要通过计算得到。这个过程称之为着色。

正因为需要逐像素计算，所以着色是局部的，也就是只研究一个像素上的着色情况。

1 光照与 Blinn-phong 反射模型

Blinn-phong 提出，模型的整体光照可以分为高光、漫反射和环境光照。

观察下面这摞茶杯，可以看到茶杯的颜色主要分为颜色变化剧烈的高光部分、颜色变化平缓的漫反射部分、没有直接光照但是被环境光线照亮的间接光照部分。

1.1 漫反射

漫反射的物体会向各个方向均匀地反射光线，不受观察方向的影响。

对于光的亮度，我们使用光的能量来表示。

根据能量守恒定律，距离光源越远，单位面积内接收到的能量就越少。而对于一个稳定散发能量的光源来说，下图中的每一个“球壳”接收到的能量应该是相同的。

设距离光源单位距离的球壳上单位面积、单位时间内接收到的能量为$I$，则距离光源$r$距离的球壳上单位面积、单位时间内接收到的能量就为

$$I_r = \frac{I}{r^2}$$

以上的假设都是基于光照垂直入射的情景，我们再将光照斜射的因素考虑进来。

当物体表面垂直于光线方向（或者说法线方向平行于光线方向）时，接收到光照的有效面积最大，接收到的能量也最多；而当物体表面平行于光线方向（也就是法线方向垂直于光线方向）时，物体接收到光照的有效面积为 0，接收到的能量也为 0。

经过很简单的几何知识可知，假设光照正射面积为$A_0$（一般设为 1），那么在斜射情况下的接收到光照的有效面积为

$$\begin{align*} A &= A_0 \cos\theta \\ &=A_0 \cdot \boldsymbol{l} \cdot \boldsymbol{n} \\ &= \boldsymbol{l} \cdot \boldsymbol{n} \end{align*}$$

不过，当光线方向和视线方向相反时，$\boldsymbol{l} \cdot \boldsymbol{n}$为负，这显然是不对的。因此，当其为负值时，就将其设为0。

$$A = \max{\{ 0,\boldsymbol{l} \cdot \boldsymbol{n} \}}$$

再考虑到物体本身的反射率$k_d$，就可得到漫反射物体上某一像素的亮度：

$$L_d = k_d \frac{I}{r^2} \max{\{0,\boldsymbol{n} \cdot \boldsymbol{l} \} }$$

1.2 高光

高光和镜面反射类似，但是也有差别。理想镜面严格遵守反射定律，即反射角等于入射角。但是高光在一个狭窄的角度范围内都能看到，并且视线方向离反射方向越近，高光越强，反之越弱。

因此，高光的重点在于视线方向$\boldsymbol{v}$和反射方向的“距离”。

你可能已经注意到，上图中出现了一个新向量$\boldsymbol{h}$。这个向量被称为半程向量，他是入射方向$\boldsymbol{l}$和视线方向$\boldsymbol{v}$的角平分线方向。我们用半程向量与法线方向$\boldsymbol{n}$的夹角$\alpha$替代我们要求视线方向$\boldsymbol{v}$和反射方向的“距离”。

不难得出：

$$\boldsymbol{h} = \frac{\boldsymbol{v}+\boldsymbol{l}}{||\boldsymbol{v}+\boldsymbol{l}||}$$

模仿漫反射的公式，高光可以如下表示：

$$\begin{align*} L_s &= k_s \frac{I}{r^2} \max{\{0,\cos\alpha\}} ^p \\ &= k_s \frac{I}{r^2} \max{\{0,\boldsymbol{n} \cdot \boldsymbol{h}\}} ^p \end{align*}$$

下图说明了$p$的作用. 当$p=1$时，我们发现，即使半程向量距离法线已经很远了，但是仍然具有可观的值，这就导致和实际情况不符合（通常我们见到到高光都是在一个很小的范围内）。因此我们加入一个指数$p$来缩小高光的可见范围。

1.3 环境光照

我们假设物体任何一个点接收到的环境光照强度都是相同的。

$$L_a = k_a I_a$$

式中的$I_a$是环境光照强度，可以近似认为一个常数，$k_a$是物体的反射率。

1.4 Blinn-Phong 反射模型

那么最后的着色结果就是把漫反射、高光、环境光照相加起来：

$$\begin{align*} L &= L_a + L_d + L_s \\ &= k_a I_a + k_d \frac{I}{r^2} \max{\{0,\boldsymbol{n} \cdot \boldsymbol{l} \} } + k_s \frac{I}{r^2} \max{\{0,\boldsymbol{n} \cdot \boldsymbol{h}\}} ^p \end{align*}$$

2 着色频率

着色频率（Shading Frequency）这个名词翻译的不好，容易让人以为它是与时间有关的概念。事实上着色频率指三种不同的位置的着色：面着色、顶点着色、像素着色。

2.1 面着色

面着色是在每一个三角形面上进行着色，每一个面的着色结果都相同。显然，这种着色并不适用于曲面。

2.2 顶点着色

你可能有些奇怪：着色的计算需要法线的参与，一个顶点哪里来的法线呢？

是的，顶点处没有法线，但是我们认为顶点的法线为相邻面的法线平均。

因为顶点相邻面的三角形有大有小，所以按照三角形面积加权。

$$\boldsymbol{n}_V = \frac{\sum \boldsymbol{n}_i}{||\sum A_i \boldsymbol{n}_i||}$$

2.3 像素着色

像素着色在顶点着色的基础上更进一步。

我们已经通过插值得到顶点处的法线，一个三角形有三个顶点，我们自然可以用这顶点处的法线插值得到三角形内任何一个像素的法线。

我们知道，由三个顶点的坐标$A,B,C$，我们可以得到三角形内任意一点的坐标$X$：

$$X = \alpha A + \beta B + \gamma C$$

其中系数满足：$\alpha + \beta + \gamma = 1$。

例如，当$\alpha = \beta = \gamma = \frac{1}{3}$时的点，就是这个三角形的重心。

一种求解系数的方法是这样的，待求点将三角形划分为三个子三角形，按照与顶点相对的原则，其面积分别设为$A_A, A_B, A_C$

于是：

$$\begin{align*} \alpha &= \frac{A_A}{A_A+A_B+A_C} \\ \beta &= \frac{A_B}{A_A+A_B+A_C} \\ \gamma &= \frac{A_C}{A_A+A_B+A_C} \\ \end{align*}$$

假设$A,B,C,X$的坐标分别为$(x_A,y_A),(x_B,y_B),(x_C,y_C),(x,y)$，则：

$$\begin{align*} \alpha &= \frac{-(x-x_B)(y_C-y_B)+(y-y_B)(x_C-x_B)}{-(x_A-x_B)(y_C-y_B)+(y_A-y_B)(x_C-x_B)} \\ \beta &= \frac{-(x-x_C)(y_A-y_C)+(y-y_C)(x_A-x_C)}{-(x_B-x_C)(y_A-y_C)+(y_B-y_C)(x_A-x_C)} \\ \gamma &= 1 - \alpha - \beta \end{align*}$$

回到法线上，设$A,B,C$三个点处的法线分别为$\boldsymbol{n}_A,\boldsymbol{n}_B,\boldsymbol{n}_C$，则任意一点$X$处的法线$\boldsymbol{n}_X为：

$$\boldsymbol{n}_X = \alpha \boldsymbol{n}_A + \beta \boldsymbol{n}_B + \gamma \boldsymbol{n}_C$$

这种插值方法被称为重心插值。

3 图形管线与着色器

3.1 图形管线

图形管线描述的是一个过程，该过程将输入的三维场景渲染绘制到屏幕上展示出来。下图展示了图形管线中的步骤：

1. 处理顶点

该部分会完成模型视图变换和投影变换。

2. 处理三角形

按照顶点之间的连接关系，绘制三角形。

3. 光栅化

将三角形光栅化为离散的像素（片元）

4. 处理片元

进行深度缓冲判断像素可见性、着色、材质映射

5. 帧缓冲操作

3.2 着色器

着色器是一种能在硬件上运行的语言，按照操作的对象不同，分为顶点着色器和片元着色器。

着色器只需要关注一个对象（顶点或者片元）的着色方式，GPU 会自动将着色器应用在每个顶点/片元处。

4 纹理映射

给一个球体贴上一张地图，这个球体就变成了地球仪。对于地球仪上的每一点，都可以在地图上找到对应的颜色。在这个例子中，地图就是纹理，而从球面坐标查找平面地图坐标的过程就是纹理映射。

在开发中，建模人员给开发人员的模型中通常会有与顶点一一对应的 UV 坐标，同时提供一张纹理贴图。比如说要对模型的某个顶点着色，这时获取到这个顶点对应的 UV 坐标，拿着这个坐标从纹理贴图中取色，取到后把值赋给存储顶点颜色的变量。

4.1 纹理重心插值

纹理映射只规定了各顶点和纹理贴图的对应关系，对于三角形内部的点，并没有准确的对应关系。

在取到三个顶点处的颜色后，使用重心插值即可得到三角形内任意一点的颜色。

4.2 双线性插值

设想这样一种情况：当纹理较小而模型较大时，纹理就要放大很多，每个像素采用最近邻法寻找最近的纹素取值，这时难免会出现锯齿。

想必你已经意识到了，应该采用插值方法缓解这种情况。

下图中的红点代表着一个像素的中心，每个格子中心的黑点代表纹素的中心。首先查找出距离像素最近的四个纹素$u00,u01,u10,u11$。

以这四个点创建新的纹理坐标系，横向为$u$方向，纵向为$v$方向，像素中心的坐标可被表示为$(s,t)$。

先看水平方向。我们发现仅在$(s,t)$这个点的垂直方向上，材质的变化从下边界的$u_0$变为上边界的$u_1$。

而$u_0$和$u_1$可以在水平方向上插值求得：

$$\begin{align*} u_0 &= u_{00} + s(u_{10} - u_{00}) \\ u_1 &= u_{01} + s(u_{11} - u_{01}) \end{align*}$$

然后，再用$u_0$和$u_1$在垂直方向上插值：

$$f(s,t) = u_0 + t(u_1 - u_0)$$

因为这种方法分别在水平方向和垂直方向上进行线性插值，因此称为双线性插值。

还有种方法取像素中心周围的 16 个纹素，在水平方向和垂直方向上进行三次插值，这种方法被称为双三次插值。

最近邻法、双线性插值、双三次插值的对比如下图所示：

4.3 Mipmap

刚才我们讨论了纹理过小的情况，但纹理是不是越大越好呢？

答案是否定的。原因我们之前提到过。纹理映射到像素上本质也是一种采样。过大的纹理意味着采样频率跟不上，就会导致走样现象。

有一种很简单的方法，因为采样频率低出现的走样现象，那我提高采样频率不就好了吗？

超采样方法固然可行，但是会消耗过多的性能。因此我们想到了缩小纹理。一个采样点的颜色信息并不能代表纹理中一个“区域”的颜色信息，那我想办法取这个区域中的平均值，不就能做到近似于点对点的映射了吗？

Level 0 为原始纹理，精度最高。随着 Level 的提升，每提升一级将 4 个相邻像素点求均值合为一个像素点，因此越高的 Level 也就代表了更大的区域。接下来要做的就是根据屏幕像素大小选定不同 Level 的纹理，再进行查询即可。而这其实就相当于在原始纹理上进行了区域查询。

接下来确定该如何选取 Level。

在屏幕空间中取当前像素点的右方和上方的两个相邻像素点，分别查询得到这 3 个点对应在纹理上的坐标。然后计算当前像素点与右方像素点和上方像素点在纹理空间中的距离$X$和$Y$：

$$\begin{align*} X = \sqrt{\left(\frac{\mathrm{d} u}{\mathrm{d} x}\right)^2+\left(\frac{\mathrm{d} v}{\mathrm{d} x}\right)^2} \\ Y = \sqrt{\left(\frac{\mathrm{d} u}{\mathrm{d} y}\right)^2+\left(\frac{\mathrm{d} v}{\mathrm{d} y}\right)^2} \end{align*}$$

然后

$$D = \log_2 \max \{ X,Y \}$$

即为需要的 Level。

但是这里算出的$D$是一个浮点数，并不是一个整数。而我们只有整数阶的 Level。这时候就要再次进行插值。

我们首先在$\lceil D \rceil$阶纹理上进行一次双线性插值，再在$\lfloor D \rfloor$阶纹理上进行一次双线性插值，然后根据这两次插值结果再进行一次插值，即可得到我们需要的纹理颜色。

$$(x,y)_{D} = (x,y)_{\lceil D \rceil} + (D-{\lfloor D \rfloor})(x,y)_{\lfloor D \rfloor}$$

这时一种三线性插值的方法。

我们将这种方法应用于这节开头的那个例子上，却发现情况并不理想，远处的纹理糊成一片：

这是因为我们给出的纹理都是横平竖直的，但是屏幕中的情况是歪七扭八的。屏幕中纵向的$D$和横向的$D$不同，才出现了这种问题。

因此我们需要进行各向异性过滤：

像这样，我们并不将横纵同时压缩，而是分别压缩横向和纵向，这样就能满足斜向要求。

这样应用之后，效果明显好了不少：

5 阴影

经过上边的分析我们知道，由于着色过程中不考虑光线的遮挡，因此在着色后只有物体的明暗变化，而没有阴影。因此阴影需要单独进行计算。

处理阴影的关键在于：不在阴影中的点必须同时被光源和相机可见。

首先分别获取光源和相机处的可见点。

然后将相机中的可见点投影回光源。当相机处可见点在光源处同样可见时，该点即正常可见；当相机处可见点在光源处不可见时，说明该点被其他物体遮挡，形成阴影。

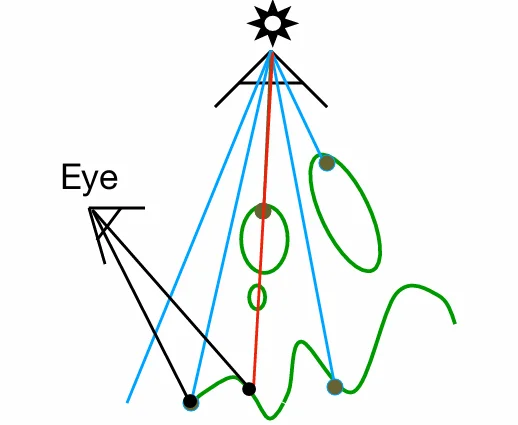
例如下面这个场景。

获取到光源处可见点，并将相机处可见点与光源处可见点对比。绿色的是两处同时可见的点，而非绿色点是不能被同时可见的点，即阴影区域。

这种方法虽然简单，但是也存在着一些问题。例如只能计算出边缘锐利的硬阴影、强依赖高质量的阴影图、浮点深度误差等。