任何模型都有其形状，我们使用曲面来描述。

1 曲面的表示方法

曲面还可分为隐式曲面与显示曲面两种。显式与隐式的区别在于所有的点是否被直接给出。

1.1 代数方程

如要表示一个球面，只需要找到所有满足

$$x^2 + y^2 + z^2 =1$$

的点即可。

即使用满足方程$f(x,y,z) = 0$的点来表示几何模型。

这种用代数方程来表示几何的方法看起来非常简洁，但是一点也不直观。（甚至有点反人类）

所以这种方法通常只用来描述简单的几何体，对于复杂的几何体则无能为力。

但是代数方程的方法也有其好处。比如，能非常方便地得到任意一个点和这个曲面的位置关系。

例如，对于上述球面，要想知道$(\frac{3}{4},\frac{1}{2},\frac{1}{4})$是否在球面上，只需要代入$f(x,y,z) = x^2 + y^2 + z^2 - 1$，发现

$$f(\frac{3}{4},\frac{1}{2},\frac{1}{4}) = -\frac{1}{8} \lt 0$$

即可立刻判断出这个点在球面内部。

1.2 构造立体几何

构造立体几何是对两个或更多的简单几何体做布尔运算。

常见的运算有并、交、差等形式。

多次运用布尔运算，可以得到代数方程无法表示（或很难表示）的几何体。

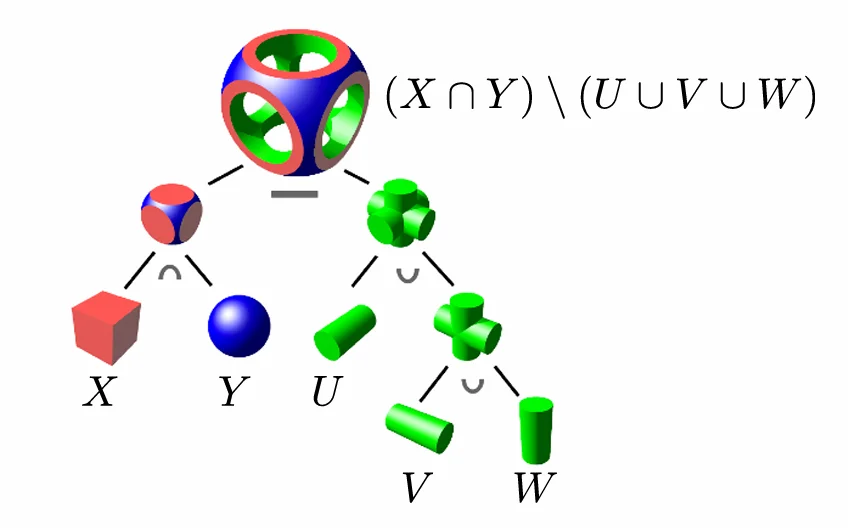
1.3 有符号距离函数

有符号距离函数并不直接表明几何的形状，而是给出空间中任意一点到几何表面的距离。当这个点的距离为正时，表明其在几何表面内部；当距离为负时在几何表面内部；当距离为 0 时，表明其恰好在表面上。

借助有符号距离函数，我们可以轻松完成下面两球融合的效果。

首先计算出空间中任意一点到两个球面的距离$SDF(A)$和$SDF(B)$，然后将$SDF(A)$和$SDF(B)$“融合”，“融合”后的值应该为正、负和 0。我们取值为 0 的点作为“融合”后的新表面，就得可以得到结果。

“融合”过程可以理解为一个取平均的过程。我们以一个阴影边界从 A 状态移动到 B状态的过程为例。

在状态 A中，右侧三分之一为阴影区域，$SDF(A)$为区域内各点到阴影边界的距离函数。我们设阴影中的点距离为负，阴影外的点距离为正，阴影边界上的点距离为 0。

状态 B 同理，只不过阴影经过移动后占了三分之二的面积。

然后我们想要得到一个从状态 A 变换到状态 B 之间的中间状态。如果我们直接将 A 和 B 做一个线性相加的话，结果就会变成图中那样三分之一黑、三分之一灰、三分之一白的情况。而正常情况下阴影移动时，肯定不会出现灰色。所以不能这么简单相加。

而如果我们对两个状态的距离函数进行融合，就会只得到正、负、0 三种情况，其中正值为白色区域，负值为黑色区域，0 为阴影边界。

这样，我们就可以做出两个几何体之间相互融合的效果。

距离函数可以表示很多圆滑的几何体。

1.4 水平集

上述方法难免涉及复杂的数学运算，简洁但是消耗大量时间去计算，难以描述复杂表面。因此我们可以用间换时间，在网格中存储近似函数，并且将插值为 0 的点作为几何表面。

相较于上述几种方法，水平集虽然也为隐式，但是其更加直观，对几何控制更加明确。

1.5 点云

点云是一系列点的坐标的集合，可以表示几乎任何复杂形状。

当然，其代价就是要使用海量点去精确描述每一个细节。如果采样点不足，就会发生走样现象。

因此点云是一种显式方法。

在得到点云后，通常会转换为多边形网格以进一步渲染。

1.6 多边形网格

多边形网格存储顶点和多边形，容易对其进行处理、模拟、自适应采样等工作。

同样，为了描述顶点和多边形的位置关系，要有一套复杂的数据结构支持。

2 网格细分

当模型的精细度不够时，我们可以对其进行超采样，得到更加细分的网格。

2.1 Loop 细分

Loop 细分用于三角形网格，分为新建三角形和调整顶点位置两步。

对于一个三角形网格，连接其三条边的中点，将其重新划分为四个三角形。

然后按照权重调整顶点位置。新顶点和旧顶点的生成方式是不同的。

对于新顶点，选取其周围的四个旧顶点$A,B,C,D$，则新顶点$X$的位置为：

$$X = \frac{3}{8} (A+B) + \frac{1}{8}(C+D)$$

对于旧顶点$A_0$，选取与其直接相连的$n$个顶点$A_1,A_2,A_3,\dots,A_n$，则旧顶点$A_0$的新位置$A_0^0$为

$$A_0^0 = (1 - nu)A_0 + u\sum_{i=1}^n A_i$$

其中，

$$u = \left\{ \begin{align*} & \frac{3}{16}, n=3 \\ & \frac{3}{8n}, otherwise \end{align*} \right.$$

2.2 Catmull-Clark 细分

Catmull-Clark 细分适用于包括三角形网格在内的所有形状的网格。下面以三角形网格和四边形网格举例。

若有$n$个顶点与某一顶点直接相连，则称该顶点的度为$n$；若$n \neq 4$，则称该点为奇异点。

首先在每个面上都添加一个顶点，然后在每条边的中点处也添加一个顶点，然后将面上的顶点连接构成该面的边上的顶点。如下图所示。

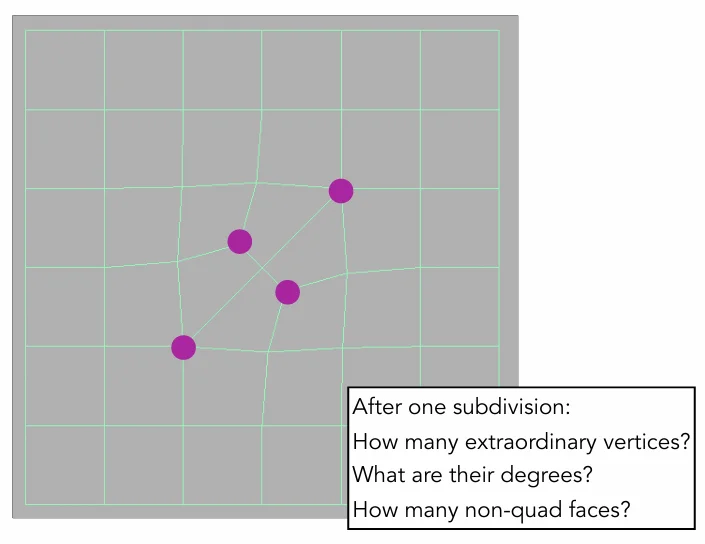
可以发现，在一次细分之后：

• 有几个非四边形面，就会多出几个奇异点
• 新奇异点的度与原来所面的边数相等
• 所有的面都会变成四边形，且奇异点数不再增加

同样的，在生成新顶点后，要调整其位置。

按照顶点的位置，我们称其为面点、边点和顶点。

对于面点$f$，取其面的四个顶点$v_1,v_2,v_3,v_4$，则：

$$f=\frac{v_1+v_2+v_3+v_4}{4}$$

对于边点$e$，取其边的两个端点$v_1,v_2$和旁边两个面的面点$f_1,f_2$，则：

$$e=\frac{v_1+v_2+f_1+f_2}{4}$$

对于旧顶点$p$，取其周围的四个面点$f_1,f_2,f_3,f_4$和与其相连的四个边的中点$m_1,m_2,m_3,m_4$，则新顶点$v$：

$$v=\frac{f_1+f_2+f_3+f_4+2(m_1+m_2+m_3+m_4)+4p}{16}$$

3 网格简化

有时一个模型面数太多，导致性能消耗巨大。这时我们可以在保持效果不发生大退步的情况下进行适度的网格简化。

通常我们使用边坍缩法简化网格。

为了评估边坍缩法对整体的影响，我们使用二次误差度量来量化其影响。其定义为，边坍缩之后的新顶点所在位置与原来各平面的距离之和。

在实际执行过程中，遍历所有的边并计算坍缩这条边之后的二次误差度量，然后找到二次度量误差最小的边并将其坍缩，然后重新遍历所有的边并坍缩最小二次度量误差的边，直至满足要求。

4 网格正则化

有时模型三角形网格分布、大小都不均匀，这在网格细分、简化、光栅化中都不方便。因此需要将三角形网格正则化，使其中的三角形大小近似、分布均匀，提高采样质量。